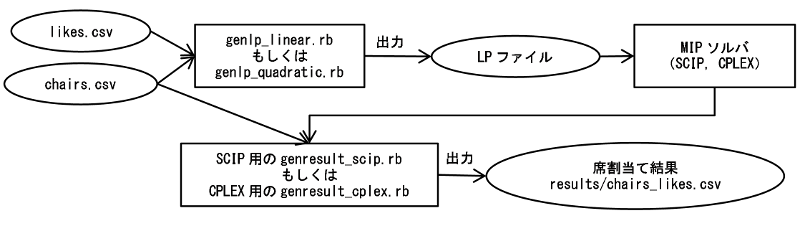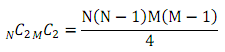席決め問題を数理計画問題として定式化する
とあるイベントにおいて参加者の座席表を作りたい．参加者は事前に誰と近くの席に座りたいかの希望をイベント主催者に提出している．イベント主催者は，開催までに参加者の希望をできるだけ叶える座席表を作成する．つまり，参加者を席に割り当てた状態と座席同士の距離，参加者の希望状況などに依存するなんらかの評価関数を定義し，それが最も良くなる場合の座席表を用意する．イベントの参加者がN人いて座席がNあるとき，全探索による解法はオーダーがO(N!)になる．イベントの参加人数は最大200人程度を想定するので，全探索による解法では全く太刀打ちできない
この席決め問題を解決できれば，小中学校のクラスの座席決めや婚活パーティなどに応用できる．こういったものの座席決めでは，生徒や参加者から不満が出やすい．もし公明正大なアルゴリズムによって最適解を求められれば，そういった不満に対して「この座席表が最も良い組み合わせだ」と主張することができる．計算機のみによる公平な座席表の作成によって，つまらない争いをなくせるかもしれない．
席決めに関して積極的でなく事前に希望をほとんど提出しない・できない人でも，有意義にイベントに参加できるようにする工夫は，次の論文中で提案されている．
[1] 西田 健志, 濱崎 雅弘, 栗原 一貴, "超消極的な人でも安心して使える学会での交流促進システム",
第20回インタラクティブシステムとソフトウェアに関するワークショップ (WISS2012)
http://www.wiss.org/WISS2012Proceedings/oral/S5_018.pdf
この論文が発表された学会の夕食では実際にシステムが運用された．私個人としては，このシステムのおかげで有意義な時間を過ごすことができ大変感謝している．
Contents |
問題の定式化
参加者には一意に識別できる番号（参加者ID）を割り当てる．また，イベント会場の座席にも一意に識別できる番号（席ID）を振る．テーブルの配置や形・大きさなどは無視し，座席の位置のみに注目する．参加人数はN人として，用意する座席数はM席とする．参加人数や座席数に上限は設けない．また，N<Mという条件を満たす必要はない（この場合は一番希望していない・希望されていない人の座席がなくなり，M-N人は会場からはじかれることになる）．
事前に，座席同士の距離を記録した次の行列dを作成する．i行j列にある要素は座席iと座席jの距離を実数で表すものとする．d(i,j)=d(j,i)のためdは上三角行列になる．dは三角不等式を満たす．
| d | 座席1 | 座席2 | 座席3 | |
|---|---|---|---|---|
| 座席1 | 0 | 座席1と座席2の距離 | 座席1と座席3の距離 | … |
| 座席2 | 0 | 座席2と座席3の距離 | ||
| 座席3 | 0 | |||
| … | 0 |
また，席の距離が近いほど目的関数（評価関数）の値が大きくなるようにしたい場合もある．d中の最大の値をMAXとして，行列D(i, j)=MAX-d(i, j)を用意する．
参加者同士の希望状況は行列Sに記録する．i行j列にある要素は参加者iの参加者jに対する希望度を表す．この希望度は0以上の任意の整数とする．この希望度合いは，適応する問題によって柔軟に変更する．例えば，[1]中の計算基準は次のように変更する．
| [1]で提案されたオリジナルの計算基準 | 変更後 | |
|---|---|---|
| 1. 既に希望がかなった2人 | -1点 | 0 |
| 2. 本人希望が存在する2人 | 2点 | 3 |
| 3. 同じ話題を希望する2人 | 2点 | 3 |
| 4. 2, 3 以外で希望が存在する2人 | 1点 | 2 |
| 5. いずれにも当てはまらない2人 | 0点 | 0 |
この計算基準を使う場合，参加者iが参加者jを希望していればS(i,j)=3になり，第三者が「参加者iが参加者jと近くの席になれたらいいな」と登録した場合S(i,j)=2になる．先ほどと同じように，S中の最大の値をMAXとして，行列s(i,j)=MAX-S(i,j) (ただしS(i,j)=0の場合はそのまま)を用意する．
ファイルフォーマット
席決め問題を表現するためのファイルの形式について説明する．
参加者の希望度合いを記録したファイル（以降likes.csvと呼ぶ）と座席の配置状況を二次元で表したファイル（chairs.csvと呼ぶ）を用意する．likes.csvは参加者からの入力を元に作成する．フォーマットを次に示す．
<参加者の人数>,, <参加者ID1>,<参加者ID2>,<希望度合いS(参加者ID1, 参加者ID2)> ・・・
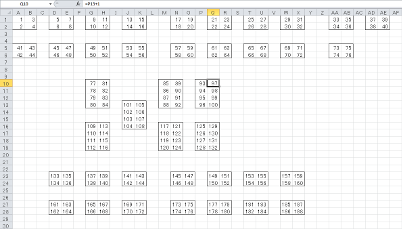
chairs.csvには席の配置状況を二次元で記録する．具体的にはCSVファイルの左上を原点にして，実際の席の配置と対応する座標のセルに座席IDを記入する．これを手作業で作るのは大変なので，表計算ソフトを方眼紙にみたてて会場を描くとよい．この作業の過程では，表計算ソフトのセル参照機能やコピー＆ペースト機能が役に立つ．
これらのプログラムとファイルの関係をまとめた結果を次に示す．
次に，後述するプログラムを用いて，座席割当て結果を表すresults/chairs_likes.csvを出力する．results/chairs_likes.csvはchairs.csvの席IDを参加者IDに置き換えたものだ．
用意したlikes.csvとchairs.csvからLPファイルを生成して，MIPソルバに問題を解かせる．ここではMIPソルバとしてSCIPとCPLEXの2つをサポートした．genlp_linear.rbは後述する整数計画問題として記述したLPファイルを出力し，genlp_quadratic.rbは2次計画問題として記述したLPファイルを出力する．SCIPの出力結果をパースして，元のchairs.csvの席IDを割当て結果の人IDに置き換えるgenresult_scip.rbとgenresult_cplex.rbも用意した．これらのプログラムとファイルの関係をまとめた結果を次に示す．
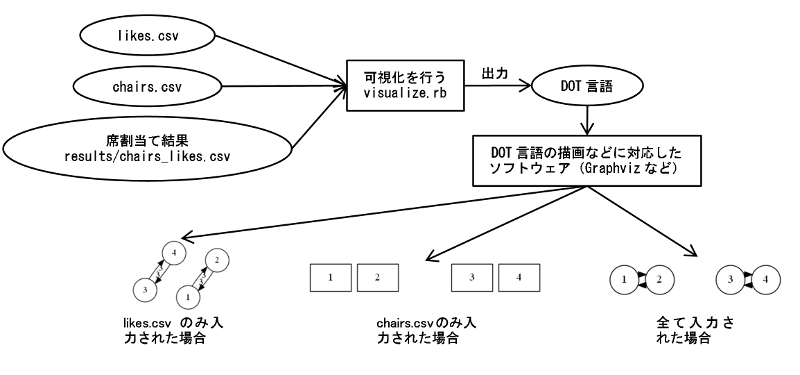
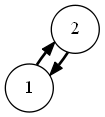
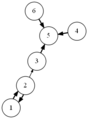
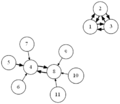
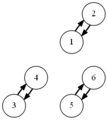
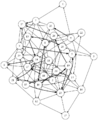
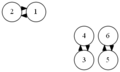
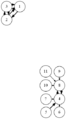
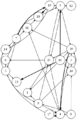
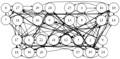
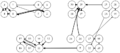
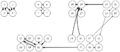
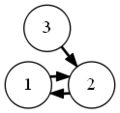
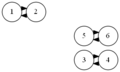
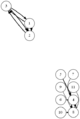
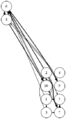
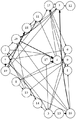
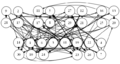
結果がcsvファイルだけでは分かりづらいので，それらを読み込んでDOT言語で記述されたグラフを出力するvisualize.rbを用意した．これにlikes.csvを入力すると参加者同士の希望状況の有向グラフを出力する．通常の希望は細い矢印で表し，強い希望は太い矢印で表す．chairs.rbを入力すると，会場の座席配置状況を出力する．これら2つと，前述の席割当て結果を合わせて入力すると，座席配置状況の上に配置された人どうしの希望状況を重ねて出力する．この図を見れば，求めた結果が本当に希望を叶えられているのかどうか確認することができる．これらのプログラムとファイルの関係をまとめた結果を次に示す．
ソースコード
作成したソースコードの一覧を次に示す．それぞれの具体的な使い方はソースコード中に記述した．
- gentestlikes.rb
- 参加者同士の希望状況をランダムに生成する
- genlp_quadratic.rb
- chairs.csvとlikes.csvをもとに2次計画問題としての定式化を出力する
- genlp_linear.rb
- chairs.csvとlikes.csvをもとに線形計画問題としての定式化を出力する
- genresult_cplex.rb
- CPLEXの出力結果をパースして座席表を出力する
- genresult_scip.rb
- SCIPの出力結果をパースして座席表を出力する
- visualize.rb
- chairs.csv, likes.csv, 求めた座席表などを可視化する
ソースコードや次で説明するテストデータセットなど関連ファイルをまとめたZIPファイル
テストデータセット
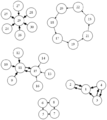
座席配置のデータセット．wiss1.csvとwiss2.csvは実際の席配置を元に作成した．
chairs/wiss1.csvの実際の会場の様子
chairs/wiss2.csvの実際の会場の様子
参加者同士の希望状況のデータセット．likes/0-8は手作業で作成し，likes/10-180はgentestlikes.rbによって生成した．
2次計画問題として解く
CPLEXを使ってこの問題を2次計画問題として解いてみよう．CPLEXはアカデミック用途に限定すると無償で使うことができる（商用ライセンスは2013年2月現在で約260万円以上する）．後述するSCIPとは違い，CPLEXは標準でマルチコアCPUを活かした分散処理が有効になっている．
求めたい解を表すバイナリ変数a(i,j)を用意する．参加者iが席jに座っている時にa(i,j)=1とする．chairs/1.csv, likes/1.csvの場合の許容解の一例を次に示す．
| a | 座席1 | 座席2 | 座席3 |
|---|---|---|---|
| 参加者1 | 0 | 1 | 0 |
| 参加者2 | 1 | 0 | 0 |
| 参加者3 | 0 | 0 | 1 |
目的関数の都合上，N=Mの制約を加える．しかし，数式を分かりやすくするために，N, Mは別々の変数として扱う．
目的関数と制約条件
chairs/1.csv, likes/1.csvに対し，行列Qの具体例を次に示す．
a(1,1) a(1,2) a(1,3) a(2,1) a(2,2) a(2,3) a(3,1) a(3,2) a(3,3) a(1,1): 0 0 0 0 1 3 0 0 0 a(1,2): 0 0 0 1 0 2 0 0 0 a(1,3): 0 0 0 3 2 0 0 0 0 a(2,1): 0 1 3 0 0 0 0 0 0 a(2,2): 1 0 2 0 0 0 0 0 0 a(2,3): 3 2 0 0 0 0 0 0 0 a(3,1): 0 0 0 0 1 3 0 0 0 a(3,2): 0 0 0 1 0 2 0 0 0 a(3,3): 0 0 0 3 2 0 0 0 0
結果
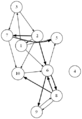
成功例
chairs/1.csv
likes/1.csv
結果
chairs/5.csv
likes/7.csv
結果
chairs/2.csv
likes/6.csv
結果
chairs/4.csv
likes/3.csv
結果
chairs/3.csv
likes/20.csv
結果
失敗例
chairs/6.csv
likes/20.csv
結果．希望の多いノードが中央に集まってしまい，参加者15は希望した相手全員と離れ離れになってしまっている．
chairs/7.csv
likes/30.csv
2時間探索を続けた所で打ち切った許容解．参加者が30人を超えるとなかなか最適解が求まらない．この場合は希望を叶えられていない参加者が目立ち，多くの太い矢印（強い希望）が会場を横断している．
探索結果を見ながら随時制約条件を追加した例
chairs/7.csv
likes/8.csv
10分間探索を行い打ち切った結果．参加者1, 2, 3, 4は同じテーブルにいた方が良さそうだ．a(1,4)=1, a(2,3)=1, a(3,1)=1, a(4,2)=1の制約条件を加える．
さらに数分間探索して打ち切った結果．参加者24, 25, 26, 27, 28, 29, 30は同じテーブルにいた方が良さそうだ．a(24,24)=1, a(25,25)=1, a(26,26)=1, a(27,29)=1, a(28,28)=1, a(29,27)=1, a(30,30)=1の制約条件を加える．
これらの制約条件のもと，10分程度放置した結果，この最適解が求まった．
整数計画問題として解く
2次計画問題として定式化するより，整数計画問題として定式化する方が多くの最適化が働き高速に解けるのではないかと考えた．ここでは，前述の2次計画問題としての定式化結果を元に，強引に整数計画問題として「定式化」する．
バイナリ変数aa(py,cy,px,cx)を用意する（これは前述のバイナリ変数aを2つくっつけたものだ）．参加者pyが席cyに座っていて，かつ，参加者pxが席cxに座っている場合にaa(py,cy,px,cx)=1とする．常にpy<px, cy<cxの条件を満たすようにする．このとき，用意する変数aaの数は
となる．参加者が180人いて，席も180席ある場合は，変数の数が259532100個になってしまう．このように，目的関数の2次式を強引に1次式に変えてしまうと，変数の数は2乗のオーダーで増加する．当然その分制約条件の記述も長くなる．参加者が多い場合はLPファイルが巨大になり，ソルバに読み込めない可能性がある．
目的関数と制約条件
aa(py,cy,px,cx)=1（人pyが席cyに座っていて，人pxが席cxに座っている状態）のとき，これの係数にはpyとpx間の希望度と距離スコアをかけたい．互いの希望度はS(py,px)S(px,py)とする．また，二人の間の距離スコアはD(cy,cx)になる．
制約条件から明らかなように，席が足りない場合は足りない席数だけ参加者が，希望順位が低い順に削られる．また，参加人数に対して席が有り余っている場合は使わない席が生じる．
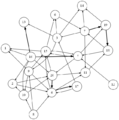
結果
chairs/1.csv
likes/1.csv
結果．参加者数が奇数の場合は参加者の内1人の座席が明示されない．この参加者は余っている座席に割り当てる
chairs/5.csv
likes/7.csv
結果
chairs/2.csv
likes/6.csv
結果
chairs/4.csv
likes/3.csv
結果．参加者が奇数人なので1人余っている．この参加者は3に座る．
chairs/4.csv
likes/10.csv
N<Mの場合であっても結果を求められる．
chairs/3.csv
likes/20.csv
おおむね希望を叶えられているが，参加者14がかわいそうに見える．
chairs/6.csv
likes/20.csv
参加者6の希望を叶えられていない．計算時間は2次計画法を使った場合とほぼ同じだった．
chairs/7.csv
likes/30.csv
結果．かかった時間は20時間程度．
結論
この文書では，席決め問題を2次計画問題・線計画問題として定式化し，最適解を求めようと試みた．
2012年2月現在で，世界1, 2位の性能を誇るMIPソルバ：CPLEXであれば，魔法のような最適化が働き，O(n!)の問題でもあっさり解けてしまうのではないかと考えていた．参加者が30人のとき，最適解を求めるまでに少なくとも20時間以上はかかる．また30人を越える場合については，1日以内に最適解を求めることはできなかった．
参加者が多い場合の席決め問題に真正面から取り組み，最適解を求めるのは難しいだろう．現在の個人用PCの性能で（比較的良さそうに見える）許容解を求めるには，山登り法やタブーサーチを使った近似解法に頼ったり，人間の直感に基づくインタラクティブな探索をする必要がある．近似解法では最適解であることを保証できないし，人間の直感に頼った操作が加わると，公平性が失われる可能性がある．この文書の冒頭で述べたような，人の手を介さない計算機のみによる公平な座席表の作成は実現できなかった．
